前言
边刷题边学
哈希表
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int i,j;
for(i=0;i<nums.size()-1;i++)
{
for(j=i+1;j<nums.size();j++)
{
if(nums[i]+nums[j]==target)
{
return {i,j};
}
}
}
return {i,j};
};
};通过两层for循环直接比对,但是时间复杂度大于使用哈希表
class Soution{
public:
vector<int> twoSum(vector<int>& nums, int target) {
map<int,int>a;//建立hash表
vector<int> b(2,-1);//用来接收数据
for(int i = 0;i<nums.size();i++){
a.insert(pair<int,int>(nums[i],i));//i是value,*it是key
}//将数据存入哈希表
for(int i=0;i<nums.size();i++)
{
if(a.count(target-nums[i])>0&&(a[target-nums[i]]!=i))
//a.count()查找map中是否存在key值,存在返回1
//a[target-nums[i]]!=i这句的效果在于如果map表中出现了重读的key值,则这个key值不能是本身
//判断是否找到目标元素且目标元素不能是本身
{
b[0]=i;
b[1]=a[target-nums[i]];
break;
}
}
return b;
}
};实现思路:
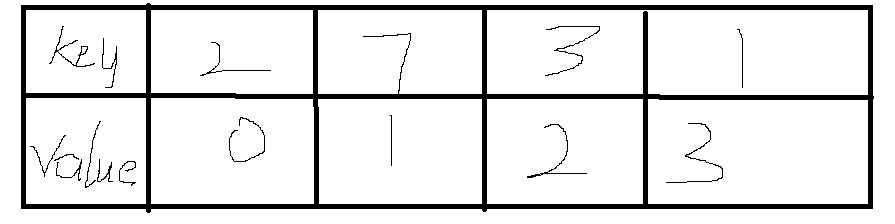
这里将数据存在哈希表中,哈希表每个key值都有一个相对于的value值
哈希表的就是用空间换时间的算法
leetcode第十三题

class Solution {
public:
int romanToInt(string s) {
int sum = 0;
int a = 0;
map<char,int> HashMap;
HashMap.insert(make_pair('I',1));
HashMap.insert(make_pair('V',5));
HashMap.insert(make_pair('X',10));
HashMap.insert(make_pair('L',50));
HashMap.insert(make_pair('C',100));
HashMap.insert(make_pair('D',500));
HashMap.insert(make_pair('M',1000));
for(int i = 0;i<s.size();i++){
if(s[i] == 'I' && s[i+1] == 'V'){
a=4;
sum +=a;
i++;
continue;
}else if(s[i] == 'I' && s[i+1] == 'X'){
a=9;
sum +=a;
i++;
continue;
}else if(s[i] == 'X' && s[i+1] == 'L'){
a=40;
sum +=a;
i++;
continue;
}else if(s[i] == 'X' && s[i+1] == 'C'){
a=90;
sum +=a;
i++;
continue;
}else if(s[i] == 'C' && s[i+1] == 'D'){
a=400;
sum +=a;
i++;
continue;
}else if(s[i] == 'C' && s[i+1] == 'M'){
a=900;
sum +=a;
i++;
continue;
}
sum = sum + HashMap[s[i]];
}
return sum;
}
};以上是我使用的笨方法,通过使用哈希表存取数据,然后再用条件判断来计算,这样写的话代码十分的臃肿(典型负面)
class Solution{
public:
int romanToInt(string s) {
int sum = 0;
map<char,int> HashMap={
{'I',1},
{'V',5},
{'X',10},
{'L',50},
{'C',100},
{'D', 500},
{'M', 1000}
};
for(int i = 0;i<s.size();i++){
if(HashMap[s[i]]<HashMap[s[i+1]])
sum -= HashMap[s[i]];
else
sum += HashMap[s[i]];
}
return sum;
}
};优秀题解
这里直接通过哈希表来取值来判断,因为在一般情况下小的数字总是在大的右边,所以就是加,通过读取哈希表,只要HashMap[s[i]]<HashMap[s[i+1]],就可以说明当前是特殊情况,小的在大的左边,应该减去小的的值,累加起来就可以得到想要的答案
2512. 奖励最顶尖的 K 名学生 - 力扣(LeetCode) 哈希加排序
class Solution {
public:
static bool cmp(pair<int,int> a, pair<int,int> b) { //在类中的自定义比较函数,必须是static类型的
if (a.first != b.first) {
return a.first > b.first;
} else {
return a.second < b.second;
}
}
vector<int> topStudents(vector<string>& positive_feedback, vector<string>& negative_feedback, vector<string>& report, vector<int>& student_id, int k) {
unordered_set<string>m1(positive_feedback.begin(),positive_feedback.end());
unordered_set<string>m2(negative_feedback.begin(),negative_feedback.end());
vector<pair<int,int>>ret;
vector<int>ans;
for(int i = 0;i<report.size();i++){
int sec = student_id[i];
string word;
istringstream ss(report[i]);
int fir = 0;
while (ss >> word) {
if(m1.find(word)!=m1.end()) {
fir += 3;
}else if(m2.find(word)!=m2.end()){
fir -= 1;
}
}
ret.push_back({fir,sec});
}
sort(ret.begin(),ret.end(),cmp);
for(int i = 0;i<k;i++) {
ans.emplace_back(ret[i].second);
}
return ans;
}
};主要是istringstream的一个操作,它可以从一个句子中提取需要的那个word
双指针
输入一行英文判断是否是回文
//回文判断
#include<iostream>
#include<string>
using namespace std;
void test(){
string str;
string str1;
string str2;
cin>>str;
int l=0;
int r = str.size()-1;
while (l<r){
str1.insert(l,1,str[l]);
//cout <<"str1 "<<str1[l]<<" "<<endl;
str2.insert(l,1,str[r]);
//cout <<"str2 "<<str2[l]<<" "<<endl;
++l;
--r;
}
if(str1.compare(str2) == 0){
cout<<"Y";
}else{
cout<<"N";
}
}
int main(){
test();
return 0;
}这里定义了两个指针,一个指向字符串的起始位置,一个指在了末位置,两个指针同时向中间移动,并将当前指向的字符存进一个字符串,跟二分查找还是蛮像的,不过好像二分查找也是通过双指针实现的,双指针算是个技巧吧。
class Solution {
public:
int maxArea(vector<int>& height) {
int l = 0;
int r = height.size()-1;
long long ans = 0;
while(l<=r){
if(height[l]<height[r]) {
ans = max(ans,(long long)height[l]*(r-l));
l++;
} else {
ans = max(ans,(long long)height[r]*(r-l));
r--;
}
}
return ans;
}
};func maxArea(height []int) int {
l := 0
r := len(height)-1
ans := 0
for l<r {
if height[l] < height[r] {
ans = max(ans,height[l]*(r-l))
l++
} else {
ans = max(ans,height[r]*(r-l))
r--
}
}
return ans
}
func max(a int,b int) int {
if a>b {
return a
} else {
return b
}
}BFS
广度优先算法
例如经典迷宫问题,在一个迷宫中输入起始位置和末位置,查找最短路径
算法思路:
先建立一个visit[] []的二维数组用于判断当前的路是否通路,全部初始化为0,走过的路赋值为1,代表不可以再走了,不是通路了
再定义一个队列用来保存当前坐标的信息,新判断的点入队,判断完成的点出队
定义坐标运动数组
int dx[4]={0,1,0,-1};//右下左上
int dy[4]={1,0,-1,0};//定义运动的坐标变化在迷宫中的某个点要向该点的上下左右四个方位进行试探,试探通路的点就移动到该点上去
核心代码
while (!r.empty())//如果当前队列不为空的话,进入循环
{
int tmpx,tmpy;
tmpx = r.front().x;
tmpy = r.front().y;//如果当前队头的坐标点等于终点坐标的位置
if(tmpx == endx && tmpy == endy){
flag = 1;
cout<<"最少的步数为"<<r.front().step;
break;
}
//开始试探四个方向
for(int k=0;k<4;k++){
int x,y;
x = r.front().x + dx[k];
y = r.front().y + dy[k];//此时的x,y就是试探后的坐标值
//如果试探当前的坐标点是通路且没有走过的
if(a[x][y] == 1 && v[x][y] == 0){
point tmpe;//将符合条件的坐标点入队
tmpe.x = x;
tmpe.y = y;
tmpe.step = r.front().step+1;
//将数据保存在临时结构体并入队
r.push(tmpe);
v[x][y] = 1;//成功入队后,该坐标点已经走过了就不是通路了,设置为1
}
}
//试探完4个方向,将队头出队,继续判断对头的下一个元素
r.pop();
}完整代码
//迷宫问题
#include<iostream>
#include<queue>
using namespace std;
int a[100][100],v[100][100]={0};//a数组用来存数据,v数组用来判断当前路是否是通路
struct point{
int x;
int y;
int step;
};//定义一个结构体其中包括坐标点的信息和当前已走的步数
queue<point> r;//定义一个队列,用来保存当前的坐标步数信息
int dx[4]={0,1,0,-1};//右下左上
int dy[4]={1,0,-1,0};//定义运动的坐标变化
void test(){
int flag = 0;//用来判断迷宫是否可以成功走出
int n,m,startx,starty,endx,endy;
cout<<"请分别输入迷宫的行列"<<endl;
cin>>n>>m;
cout<<"请输入迷宫"<<endl;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
cout<<"请输入分别输入起始坐标的x,y与终点坐标的x,y"<<endl;
cin>>startx>>starty>>endx>>endy;
point start;//定义刚开始位置的结构体
start.x = startx;
start.y = starty;
start.step = 0;
v[startx][starty] = 1;//把当前位置的设置为通路
r.push(start);//将第一个点入队
while (!r.empty())
{
int tmpx,tmpy;
tmpx = r.front().x;
tmpy = r.front().y;//如果当前队头的坐标点等于终点坐标的位置
if(tmpx == endx && tmpy == endy){
flag = 1;
cout<<"最少的步数为"<<r.front().step;
break;
}
//开始试探四个方向
for(int k=0;k<4;k++){
int x,y;
x = r.front().x + dx[k];
y = r.front().y + dy[k];
//如果试探当前的坐标点是通路且没有走过的
if(a[x][y] == 1 && v[x][y] == 0){
point tmpe;
tmpe.x = x;
tmpe.y = y;
tmpe.step = r.front().step+1;
//将数据保存在临时结构体并入队
r.push(tmpe);
v[x][y] = 1;
}
}
//一个循环结束后,将队头出队
r.pop();
}
if(flag!=1){
cout<<"查找最短路径失败";
}
}
int main(){
test();
return 0;
}回溯算法
模板
void backtracking(条件){
if(){
//结束判断
}
for(){//遍历子问题
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}排列问题
全排列
class Solution {
public:
vector<vector<int>>ans; //返回
vector<int>path; //记录结果
void backtracking(vector<int> nums,vector<bool> cnt){
if(path.size() == nums.size()) { //边界条件
ans.push_back(path);
return;
}
for(int i = 0;i<nums.size();i++) {//遍历子问题
if(cnt[i] == true) continue; //如果被遍历过
cnt[i] = true;
path.push_back(nums[i]);
backtracking(nums,cnt);
path.pop_back(); //回溯
cnt[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<bool>cnt(nums.size(),false);
backtracking(nums,cnt);
return ans;
}
};func permute(nums []int) [][]int {
var ans [][]int
var path []int
cnt := make([]bool, len(nums))
var backtracking func(nums []int, cnt []bool)
backtracking = func(nums []int, cnt []bool) {
if len(path) == len(nums) {
temp := make([]int, len(path))
copy(temp, path)
ans = append(ans, temp)
return
}
for i := 0; i < len(nums); i++ {
if cnt[i] {
continue
}
cnt[i] = true
path = append(path, nums[i])
backtracking(nums, cnt)
path = path[:len(path)-1]
cnt[i] = false
}
}
backtracking(nums, cnt)
return ans
}组合问题
class Solution {
public:
vector<vector<int>>ans;
vector<int>path;
vector<vector<int>> combine(int n, int k) {
backtracking(n,k,1);
return ans;
}
void backtracking(int n,int k,int index){
if(path.size() == k){
ans.push_back(path);
return;
}
for(int t = index;t<=n;t++){
path.push_back(t);
backtracking(n,k,t+1);
path.pop_back();
}
}
};func combine(n int, k int) [][]int {
var ans [][]int
var path []int
var backtracking func(n int ,k int,index int)
backtracking = func(n int ,k int,index int) {
if len(path) == k {
temp := make([]int ,len(path))
copy(temp,path)
ans = append(ans,temp)
}
for t := index;t<=n;t++ {
path = append(path,t)
backtracking(n,k,t+1)
path = path[:len(path)-1]
}
}
backtracking(n,k,1)
return ans
}class Solution {
public:
string m[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string>ans;
string path;
void backtracking(string digits,int index){
if(path.size() == digits.size()){
ans.push_back(path);
return;
}
int t = digits[index] - '0';
string temp = m[t];
for(int i = 0;i<temp.size();i++){
path.push_back(temp[i]);
backtracking(digits,index+1);
path.pop_back();
}
}
vector<string> letterCombinations(string digits) {
if(digits.size() == 0){
return {};
}
backtracking(digits,0);
return ans;
}
};动态规划
当一个问题有多个重叠的小问题,每一个状态都是由上一个状态推导而来的。
动规五部曲
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
01背包问题,小明有一个容量为m的书包,现有物品A,B,C三件有不同的重量和价值,求在小明书包容量下可以装的最大价值装法
//背包01问题
#include<iostream>
#include<vector>
using namespace std;
int max(int a,int b){
return a>b?a:b;
}
void test(){
int num,bagweight;
cout<<"请输入商品的数量和背包大小"<<endl;
cin>>num>>bagweight;
vector<int>wight(num);
vector<int>value(num);
cout<<"请输入商品信息(先输入体积再价值)"<<endl;
for(int i =0;i<num;i++){
cin>>wight[i];
cin>>value[i];
}
//定义一个二维数组用于记录数据
vector<vector<int>> dp(wight.size(),vector<int>(bagweight+1,0));
//该dp的含义是在0~i中选取i个物品装进j容量的背包中
//初始化第一行和第一列
for(int j=wight[0];j<=bagweight;j++){
dp[0][j] = value[0];
}
//weight数组的大小就是物品个数
for(int i=1;i<wight.size();i++){//先遍历物品,这里因为第一行已经全部初始话所以,从i=1开始遍历
for(int j =0;j<=bagweight;j++){//遍历背包容量
if(j<wight[i]){//如果背包的容量小于物品的重量,就不拿i物品
dp[i][j] = dp[i-1][j];
}else{//拿物品
dp[i][j] = max(dp[i-1][j],dp[i-1][j-wight[i]]+value[i]);
}
}
}
cout << dp[wight.size() - 1][bagweight] << endl;//最后一格即使最优的解
}
int main(){
test();
return 0;
}leetcode70题

class Solution {
public:
int climbStairs(int n) {
if(n<=1){
return n;
}
vector<int>a(n+1);//这里要+1因为物理空间大小和逻辑空间大小差1
a[1] = 1;
a[2] = 2;
for(int i = 3;i<n;i++){
a[i] = a[i-1] +a[i-2];
}
return a[n];
}
};Dijkstra
迪杰斯特拉算法
用于找出单源的最小路径问题
#include<iostream>
#define V 20 //顶点的最大个数
#define INFINITY 65535
typedef struct{
int vexs[V]; // 储存图中的顶点数据
int arcs[V][V]; //二维数组记录顶点之间的关系
int vexnum,arcnum; // 记录图的顶点数和弧数
}MGraph;
//根据顶点本身的数据,判断出顶点在二维数组中的位置
int LocateVex(MGraph* G,int v){
int i=0;
for(;i<G->vexnum;i++){
if(v == G->vexs[i]){
break;//遍历数组找到位置
}
}
if(i>G->vexnum){
std::cout<<"not find"<<std::endl;
return -1;
}
return i;
}
//构造无向有权图
void Init_GM(MGraph* G){
std::cout<<"请输入顶点数和边数"<<std::endl;
std::cin>>G->vexnum>>G->arcnum;
std::cout<<"请输入各个顶点"<<std::endl;
for(int i=0;i<G->vexnum;i++){
std::cin>>G->vexs[i];
}
for(int i=0;i<G->vexnum;i++){
for(int j=0;j<G->vexnum;j++){
G->arcs[i][j] = INFINITY; // 初始化一开始的距离
}
}
std::cout<<"输入每个边的数据"<<std::endl;
for(int i=0;i<G->arcnum;i++){
int v1,v2,w;//边关联的两个顶点和权值
std::cin>>v1>>v2>>w;
int n=LocateVex(G,v1);
int m=LocateVex(G,v2);
if(n==-1 || m==-1) return;
G->arcs[n][m] = w;
G->arcs[m][n] = w;
}
}
//迪杰斯特拉算法
void Dijkstra_minTree(MGraph G,int v0,int p[V],int d[V]){ // v0代表其实坐标点的数组下标
int find_min[V]; // 判断各个顶点是否已经是最短路径
for(int i=0;i<G.vexnum;i++){
find_min[i] = 0;
d[i] = G.arcs[v0][i];
p[i] = 0;
}
d[v0] = 0;
find_min[v0] = 1;
int k = 0;
for(int i=0;i<G.vexnum;i++){
int min = INFINITY;
for(int w=0;w<G.vexnum;w++){
if(!find_min[w]){
if(d[w]<min){
k = w;
min = d[w];
}
}
}
find_min[k] = 1;
for(int w=0;w<G.vexnum;w++){
if(!find_min[w] && (min+G.arcs[k][w] < d[w])){
d[w] = min + G.arcs[k][w];
p[w] = k;
}
}
}
}
int main(){
MGraph G;
Init_GM(&G);
int p[V];
int d[V];
Dijkstra_minTree(G,0,p,d);
}两版
#include <iostream>
#include <vector>
#include <queue>
#include <limits.h>
// 使用标准命名空间
using namespace std;
// 定义边
struct Edge {
int to; // 目标节点
int weight; // 边权重
// 构造函数,初始化目标节点和边权重
Edge(int t, int w):to(t), weight(w){}
};
// 定义图
typedef vector<vector<Edge>> Graph;
// 定义距离数组
typedef vector<int> Distance;
// 迪杰斯特拉算法,求从起点出发到其他各个节点的最短距离
Distance dijkstra(const Graph& graph, int source) {
const int n = graph.size(); // 图中节点数目
Distance distances(n, INT_MAX); // 初始化距离数组,全为INT_MAX
distances[source] = 0; // 初始节点到自身距离为0
// 使用小根堆维护每个节点距离起点的距离
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;
heap.push(0, source); // 将起点加入堆中,距离为0
while (!heap.empty()) {
// 取出堆顶元素(当前距离起点最近的节点)
pair<int, int> p = heap.top();
heap.pop();
int node = p.second, distance = p.first;
// 如果该节点已被访问过,则跳过之
if (distances[node] < distance) {
continue;
}
// 更新邻居节点距离,并加入堆中
for (const Edge& edge : graph[node]) {
int neighbor = edge.to, weight = edge.weight;
int new_distance = distance + weight;
if (new_distance < distances[neighbor]) {
distances[neighbor] = new_distance;
heap.push(new_distance, neighbor);
}
}
}
return distances; // 返回起点到各节点的最短距离数组
}
// 主函数
int main() {
// 定义示例图
Graph graph(5); // 图中有5个节点
graph[0].push_back(Edge(1, 10)); // 0号节点到1号节点距离为10
graph[0].push_back(Edge(4, 5)); // 0号节点到4号节点距离为5
graph[1].push_back(Edge(2, 1)); // 1号节点到2号节点距离为1
graph[1].push_back(Edge(4, 2)); // 1号节点到4号节点距离为2
graph[2].push_back(Edge(3, 4)); // 2号节点到3号节点距离为4
graph[3].push_back(Edge(0, 7)); // 3号节点到0号节点距离为7
graph[3].push_back(Edge(2, 6)); // 3号节点到2号节点距离为6
graph[4].push_back(Edge(1, 3)); // 4号节点到1号节点距离为3
graph[4].push_back(Edge(2, 9)); // 4号节点到2号节点距离为9
graph[4].push_back(Edge(3, 2)); // 4号节点到3号节点距离为2
Distance distances = dijkstra(graph, 0); // 以0号节点为起点,求最短距离
// 打印起点到各点的最短距离
for (int i = 0; i < distances.size(); i++) {
cout << "Distance from 0 to " << i << " is " << distances[i] << endl;
}
return 0; // 返回程序执行成功状态
}单调栈
class Solution {
public:
//单调栈模板题目
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
vector<int>ret(n);
stack<int>ss; //储存下标
for(int i = 0;i<n;i++) {
while(!ss.empty() && temperatures[i] > temperatures[ss.top()]){
int j = ss.top();
ss.pop();
ret[j] = i-j;
}
ss.push(i);
}
return ret;
}
};func dailyTemperatures(temperatures []int) []int {
n := len(temperatures)
ss := []int{}
ret := make([]int,n)
for i:=0;i<n;i++ {
for len(ss) > 0 && temperatures[i] > temperatures[ss[len(ss)-1]] {
j := ss[len(ss)-1]
ss = ss[:len(ss)-1]
ret[j] = i - j
}
ss = append(ss,i)
}
return ret
}前后缀和
42. 接雨水 - 力扣(LeetCode) 这题解法很多
class Solution {
public:
int trap(vector<int>& height) {
//前,后缀和解法
int n = height.size();
vector<int>per(n,0);
per[0] = height[0];
vector<int>suf(n,0);
suf[n-1] = height[n-1];
int ans = 0;
for(int i = 1;i<n;i++) {
per[i] = max(per[i-1],height[i]);
}
for(int i = n-2;i>=0;i--) {
suf[i] = max(suf[i+1],height[i]);
}
for(int i=0;i<n;i++)
ans += min(per[i],suf[i]) - height[i];
return ans;
}
};func trap(height []int) int {
n := len(height)
per := make([]int,n)
suf := make([]int,n)
per[0] = height[0]
suf[n-1] = height[n-1]
var ans int = 0
for i:=1;i<n;i++ {
per[i] = max(per[i-1],height[i])
}
for i:=n-2;i>=0;i-- {
suf[i] = max(suf[i+1],height[i])
}
for i:=0;i<n;i++ {
ans += min(per[i],suf[i]) - height[i]
}
return ans
}
func min(a int,b int) int {
if(a<b) {
return a
}else {
return b
}
}
func max(a int,b int) int {
if(a>b) {
return a
}else {
return b
}
}前后缀积 思想是一样的
238. 除自身以外数组的乘积 - 力扣(LeetCode)
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> ans(n);
vector<long long> pre(n);
vector<long long> beh(n);
pre[0] = 1; // 将pre[0]初始化为1
beh[n-1] = 1; // 将beh[n-1]初始化为1
// 计算pre数组
for(int i = 1; i < n; i++){
pre[i] = nums[i-1] * pre[i-1];
}
// 计算beh数组
for(int i = n-2; i >= 0; i--){
beh[i] = nums[i+1] * beh[i+1];
}
// 计算结果数组ans
for(int i = 0; i < n; i++){
ans[i] = pre[i] * beh[i];
}
return ans;
}
};func productExceptSelf(nums []int) []int {
n := len(nums)
ans := make([]int,n)
pre := make([]int,n)
beh := make([]int,n)
pre[0] = 1;
beh[n-1] = 1;
//前缀
for i:=1;i<n;i++ {
pre[i] = pre[i-1]*nums[i-1]
}
//后缀
for i:=n-2;i>=0;i-- {
beh[i] = beh[i+1]*nums[i+1]
}
for i:=0;i<n;i++ {
ans[i] = pre[i] * beh[i]
}
return ans
}滑动窗口
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int ans = 0;
int left = 0;
unordered_map<char,int>m; //使用hash表记录字符的出现次数
for(int right = 0;right<s.size();right++) {
m[s[right]]++; //记录
while (m[s[right]] > 1) { //如果出现次数大于1
m[s[left]]--;
left++;
}
ans = max(ans,right-left+1);
}
return ans;
}
};func lengthOfLongestSubstring(s string) int {
ans := 0
left := 0
m := make(map[byte]int)
for right:=0;right<len(s);right++ {
m[s[right]]++
for m[s[right]] > 1 {
m[s[left]]--
left++
}
ans = max(ans,right-left+1)
}
return ans
}
func max(a int,b int)int {
if(a>b){
return a
}else {
return b
}
}class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int ans = INT_MAX;
int l = 0;
long long sum = 0;
for(int r = 0;r<nums.size();r++) {
sum+=nums[r];
while(sum>=target){
sum-=nums[l];
ans = min(ans,r-l+1);
l++;
}
}
return (ans!=INT_MAX)?ans:0;
}
};438. 找到字符串中所有字母异位词 - 力扣(LeetCode)
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
//hash表存储p中出现字符
int m[26] = {0};
int curm[26] = {0};
//vector<int>m(26,0);
//vector<int>curm(26,0);
if(s.size()<p.size()) return {};
for(auto i:p){
m[i-'a']++;
}
int n = p.size();
for(int i = 0;i<n-1;i++){
curm[s[i]-'a']++;
}
vector<int>ans;
int l = 0;
for(int r = n-1;r<s.size();r++){
curm[s[r]-'a']++;
if(!memcmp(m,curm,sizeof(m))){ //普通数组不能直接用m == curm,用普通数组主要是能优化4ms(岂不美哉)
ans.push_back(l);
}
curm[s[l]-'a']--;
l++;
}
return ans;
}
};模板
int left = 0;
int ans = 0;
for (int right = 0;right<len;right++) {
//操作
while(//题目条件){
//操作
l++
}
}

